חלוקת נכסים מוחשיים יעילה וללא קנאה

חיקם ביתן, כלכלן, סטטיסטיקאי מוסמך במינהל עסקים ושמאי מקרקעין

תקציר :

המאמר מציע מודל חדשני לחלוקת נכסים מוחשיים בלתי ניתנים לחלוקה (כגון דירות מגורים) בין שותפים, באופן שהוא  יעיל פרטו ונטול קנאה צולבת. המודל מציע תהליך חלוקה מבוסס העדפות סובייקטיביות תוך שימוש באלגוריתם ההונגרי (בגרסה הממקסמת).

הבסיס למודל הוא שמאות מקרקעין אובייקטיבית לכל נכס, אשר נמסרת לבעלים. כל אחד מהבעלים מביע את העדפותיו באמצעות שינוי ערך השמאות כלפי מעלה (העדפה), מטה (דחייה) או השארה ללא שינוי (אדישות). יודגש כי שומה זו משמשת כבסיס להעדפות האישיות בלבד ואינה לוקחת חלק בהמשך התהליך. נתוני ההעדפות של כל הבעלים נשמרות במטריצה . מטריצה זו מייצרת העדפה אישית, לפיה נבנית הקצאה שממקסמת את סך הערך שמקבל כ"א מהבעלים.

השלב הבא הוא זיהוי קנאה צולבת – מצבים שבהם בעלים אחד מעדיף את הקצאתו של בעלים אחר. פתרון הבעיה נעשה דרך "קופה" (פרדוקס הערך) – עודף שנוצר מהבדלים בין ההערכות הסובייקטיביות לערך הכולל של ההקצאה המרבית. הקופה משמשת לתיקון הקנאה.  במקרה נדיר שבו הקופה אינה מספיקה, ניתן להגיע להקצאה כמעט נטולת קנאה

בנוסף, המודל מציע מנגנון למניעת ניצול המערכת באמצעות הגבלת סכום ההערכות הסובייקטיביות לכל בעלים לסך הערכת השמאות, כדי לשמר הוגנות ולמנוע מניפולציות

המודל מדגיש שחלוקה צודקת אינה תלויה במזל (כבהגרלה), אלא בשיקול דעת ובהעדפות פרטניות. התוצאה היא חלוקה הוגנת, יעילה, נטולת קנאה ופסיכולוגית משביעת רצון  שבה כל צד מקבל יותר ממה שחשב שמגיע לו לעומת הגרלה שיוצרת בד"כ הרגשת קיפוח ואי שביעות רצון אצל האחרונים בהגרלה.

1. מבוא

1.1 אחת המשימות היותר קשות והמורכבות של בעלי מקצוע בתחום המקרקעין היא חלוקת נכסים מוחשיים בין בעליהם באופן הוגן וללא קנאה. הנכסים יכולים להיות כל אחד מהבאים : יצירות אומנות, רכבים וכמובן נכסי מקרקעין שאינם ניתנים חוקית או פיזית לחלוקת משנה. מטבע הדברים מאמר זה יעסוק בחלוקת נכסי מקרקעין בכלל ובדירות מגורים בפרט. הנחת הבסיס ההכרחית היא כי הנכסים או הדירות אינן ניתנות לחלוקת משנה כגון פיצול הן מבחינה חוקית והן מבחינה פיזית.

1.2 שיטת החלוקה השוררת כיום בישראל היא באמצעות קביעת ניקוד או שווי שמאי לכל אחת מהיחידות לחלוקה ולאחריה הגרלה לקביעת סדר הבחירה של כל אחד מהבעלים. כאמור הגרלה היא שיטת הימורים טהורה גם אם הזוכה נבחר בבחירה אקראית לחלוטין לכאורה צודקת. ההנחה הבסיסית על ההתנהגות האנושית היא שכאשר מדובר בסכומי ערך גבוהים הפרט יוגדר כשונא סיכון. כפי שאוכיח בהמשך שיטה זו הגם שהיא לכאורה הוגנת, פשוטה ומובנת מביאה לקנאה צולבת בין חלק מחברי הקבוצה ולקיפוח חלק מחברי הקבוצה. ההגדרה לקנאה צולבת והסבר כיצד היא נמדדת בהמשך המאמר. אין צורך לחזור על הקלישאה כי "בהגרלה הראשונים מרוצים והאחרונים בוכים".

1.3 השיטה המוצעת במאמר זה שומרת על שני עקרונות : יעילות פרטו וביטול הקנאה הצולבת.

עקרון פרטו, הקרוי על שם הכלכלן האיטלקי וילפרדו פרטו, קובע כי הקצאה נחשבת ליעילה כאשר לא ניתן לשפר את מצבו של שותף אחד מבלי לפגוע במצבו של שותף אחר. במילים אחרות, אם שינוי בחלוקה מיטיב עם אחד – אך בהכרח מרע עם אחר – הרי שההקצאה המקורית הייתה יעילה פרטו. עקרון זה מהווה יסוד בתכנון חלוקות הוגנות: אם כל שותף מקבל לפחות לפי העדפותיו ואין אפשרות לבצע שינוי שייטיב עם אחד בלי לקפח את השני, אזי מדובר בחלוקה ראויה ויציבה.

1.4 השיטה המתוארת במאמר משלבת בין השאיפה למקסם את שביעות הרצון של כל שותף לבין הרצון למנוע קנאה. בתחילה נערכת הקצאה שמביאה למקסימום את הערך הסובייקטיבי הכולל של ההקצאה (יעילות פרטו). משלב השני מחושב הערך רך שכ"א מהבעלים שחשב שמגיע לו. ערך זה מוחסק מגובה ההקצאה שלו . הערך נטו משמש לבחינת הקנאה.. אם מתגלה קנאה, נעשה שימוש בסכום החיובי שנוצר עקב ההפרשים בין מה שצריך להיות משולם למי מהבעלים לבין הסכום שמי מהבעלים צריך לשלם ("קופה"). כדי לתקן את תחושת הקיפוח ולנטרל את הקנאה משתמשים בכספים שנצברו בקופה.. ההליך חוזר עד שכל השותפים שבעי רצון מהקצאה, איש מהם אינו מקנא ברעהו, ומתקבלת הקצאה שהיא הוגנת, יעילה פרטו, וגם יציבה. הקופה נוצרת לאור ההקצאה היעילה.

1.5 ההקצאה נעשית ע"י שימוש בעקרונות האלגוריתם ההונגרי(Hungarian Algorithm)  אלא שבמקום למצוא מינימום מוצאים הקצאה מקסימלית.

האלגוריתם ההונגרי הוא שיטה לפתרון בעיית השמה אופטימלית (Assignment Problem), שבה רוצים לשבץ עובדים למשימות כך שסך העלות יהיה מינימלי (או הרווח מקסימלי). האלגוריתם פותח בשנות ה-50 ומבוסס על עיבוד מטריצת עלויות. הוא פועל בשלבים: מחסיר ערכים בשורות ועמודות, מוצא כיסויים מינימליים של אפסים, ומשנה את המטריצה עד שמתקבל פתרון אופטימלי. זמן הריצה שלו הוא סביר. הוא משמש בתחומים כמו לוגיסטיקה, כלכלה ,הקצאת נכסים ובינה מלאכותית.

האלגוריתם ההונגרי מיועד למקסם את הערך הכולל של הקצאה בין הבעלים, בהתבסס על מטריצת ערכים סובייקטיבית.

1.6 נסביר כיצד נוצרת הקנאה  הצולבת: כל בעלים יודע איזה נכס הוקצה לכ"א מיתר חברי הקבוצה ואת תשלומי האיזון של כ"א מיתר חברי הקבוצה האמור לשלם או לקבל.  הוא כמובן יודע וזוכר את העדפותיו האישיות שלו לנכס שקיבל והערך שנתן לנכסים שלא קיבל. לכ"א מיתר הנכסים שקיבלו חברי הקבוצה הוא מחסיר או מוסיף  את תשלום האיזון.  במקרה שהשווי נטו שקיבל נמוך מהשווי נטו שקיבל האחר לפי העדפותיו נטו  הוא "מכריז" על הקנאה.

1.7 המערכת שהוצגה במאמר זה מזהה אוטומטית מקרים של קנאה צולבת, ומסווגת אותם ככשל מערכת. כדי לבטל את הקנאה, מוצע מנגנון פיצוי המבוסס על "קופת איזון" – תוספת משותפת שממנה ניתן לבעלים המקנא, מבלי לשנות את ההקצאה עצמה. גובה הפיצוי נקבע לפי עוצמת הפער בין השווי נטו שהוצע לבין השווי נטו שהוקצה לבעלים בו הוא מקנא, ולעיתים לפי מספר ההקצאות הבעייתיות שבהן שחקן מופלה. פתרון זה משמר את יתרונות האלגוריתם ההונגרי מבחינת יעילות, תוך תיקון העיוותים שהוא עלול לגרום לעיתים קרובות לרבות בדוגמה המוצגת במאמר זה. הסבר על דרך החישוב בהמשך.כך נוצרת מערכת הקצאה הוגנת שאינה מסתפקת במקסימום טכני, אלא בוחנת גם את צדק החלוקה מנקודת ראות פרטנית

1.8 במקרה שמספר הנכסים העומדים לחלוקה זהה למספר הבעלים לכל אחד מהבעלים תוקצה דירה אחת. כאשר  מספר הבעלים גבוה מכמות הדירות חלק מהבעלים יקבל תמורה כספית מתוך תשלומי האיזון של אלה שלהם הוקצתה דירה. לעומת זאת אם מספר הדירות גבוה ממספר הבעלים קיימת אפשרות להקצאת יותר מדירה אחת למי מהבעלים או לייצור "דירת שאריות" כדי להימנע משלומי האיזון  .

1.9 נקודה אחרונה להקדמה זו היא כי נדרשת והכרחית שומה של שמאי מקרקעין לכל הדירות המיועדות לחלוקה. שומה זו תשמש נקודת ייחוס לבעלי הזכויות ובתהליך שאני מציע במאמר זה שמורה להם הזכות לאמץ או לדחות (כלפי מעלה או כלפי מטה) את שומת השמאי לכל אחת מהדירות. דחיית השומה כלפי מעלה (ערך גבוה משומת השמאי) משמעה שהפרט מעדיף דירה זו במיוחד . דחיית השומה כלפי מטה משמעה שהפרט סולד מדירה זו ואינו מעוניין לזכות בה. קבלת שווי הדירה משמעו שהבעלים אדיש אם לקבלה אם לאו.

2. פרדוקס תוספת השווי

בעת חלוקת דירות או נכסים מוחשיים אחרים בין מספר בעלים, נוצר פרדוקס מפתיע:  הקופה נוצרת מההפרש של ההקצאות בפועל לבין ההערכה הסובייקטיבית שכ"א מהבעלים מעריך שמגיע לו . כל שותף מעריך באופן אינטואיטיבי את "חלקו ההוגן" ומצפה לקבל הקצאה שתשקף תחושה זו . בשלב הראשון הוא אכן זוכה לערך זה בדיוק .

תופעה זו, אותה ניתן לכנות "פרדוקס הערך", מבטאת את הפער בין מה שכל אחד מהבעלים חשב שמגיע לו, בהתבסס על תחושותיו, העדפותיו, רגשות בעלות או זיקה לדירות מסוימות – לבין שווי הנכס שהוקצה לו בפועל לפי העדפתו הגבוה. ככל שהעדפות הבעלים נבדלות זו מזו, כך מתרחב גם הפער בין סך ההערכות הסובייקטיביות לבין השווי הכללי של הנכסים – וכך נוצר עודף ערך מצטבר בתהליך ההקצאה.

מטרת מודל זה לייצור מערכת בה כ"א אחד מהבעלים יקבל ערך אשר לפי הערכתו האישית גבוה יותר ממה שחשב שמגיע לו לפי חלקו היחסי. הדבר גורם לכך שכל אחד מהצדדים יוצא מרוצה מההקצאה (("Win-Win Situation. במילים אחרות – מתוך המגוון הקוגניטיבי והרגשי נולד רווח קולקטיבי, שמאפשר את פתרון הקנאה ומוביל לחלוקה הוגנת ויציבה.

המודל המוצג במאמר זה עושה שימוש בתופעה זו: הוא ממקסם את סך ההערכות הסובייקטיביות של הבעלים, וכאשר נותר עודף ערך – המשמש להפחתת קנאה בין הבעלים. בסופו של תהליך, כל אחד מהצדדים מקבל ערך הגבוה מזה שייחס לעצמו בתחילת הדרך – ועל כן נוצר אפקט פסיכולוגי של שביעות רצון, למרות המורכבות הבין-אישית שבחלוקה

תהליך החלוקה דורש כאמור שומת מקרקעין מפורטת אשר תקבע את שווי כל אחד מהנכסים, במקרה שלנו דירות. שומה זו תומצא לכל אחד מבעלי הנכסים.

כל אחד מבעלי הדירות יכול להתייחס לכל אחת מהדירות בשלשה אופנים שונים בהתאם להעדפותיו האישיות .

1. לדירה מסוימת שהוא מעדיף ורוצה להגדיל את סיכוייו לזכות בה בהקצאה ייתן  ערך גבוה משומת השמאי.

2. לדירה שהוא סולד ממנה ואינו חפץ בהקצאתה אליו ייתן סכום נמוך משומת השמאי.

 3. לדירה שהוא אדיש ביחס אליה לא ישנה את שומת השמאי.

בטבלה הבאה מטריצה של 5 בעלים עם 5 דירות. מטריצה זו תשמש מאמר זה לבחינת משמעות תוצאות ההגרלה ומנגד החלוקה ללא קינאה. לצורך הדוגמה בלבד זכויות כל אחד מהבעלים מהווה 20% מסה"כ השווי. כמובן שניתן לקבוע זכויות שונות למי מהבעלים בתנאי כמובן שהסכום יהיה 100%.

בטבלה זו פירוט הערכת השמאי וההתייחסות הדיסקרטית של כל אחד מהבעלים בהתאם להעדפותיו. לדוגמה בעלים 2 מעדיף במיוחד את דירה אחת ולכן "נתן" לה ערך הגבוה ב- 7.8% יותר משומת השמאי. לעומת זאת בעלים 4 אינו מעוניין לקבל את דירה 1 ו"נתן" לה ערך הנמוך משומת השמאי  של כ- 91.3% מהערכת השמאי.(הערכים בטבלה באלפי ₪).

מאחר ולמערכת חלוקה זו קיימת תכנה ייעודית לביצוע המשימה המלל הוא באנגלית.

הערכי בטבלה באלפי ₪.

בשיטת ההקצאה נושא מאמר זה תערך בחינה של ההקצאה אשר תניב את הסכום המירבי של השווי הסובייקטיבי של הבעלים. שיטת הקצאה זו היא היפוך האלגוריתם ההונגרי באופן שסה"כ שווי ההקצאות הסובייקטיבי יהיה מירבי.

להלן תוצאת ההקצאה שמקיימת את התנאי האמור (יעילות פרטו) :

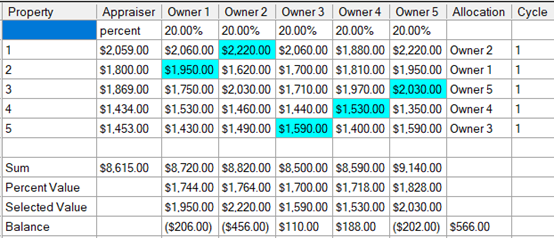
שווי של הערכות הבעלים כפי "שמגיע" להם לפי העדפותיהם הוא 8,754 אלפי ₪ . שווי ההקצאה הכולל לפי ההעדפות הבעלים הוא 9,320 אלפי ₪ . ההפרש של 566 אלפי ₪ מהווה את פרדוקס גידול הערך. פרדוקס גידול הערך נובע מההעדפות השונות של הבעלים. סכום זה יישמר "בקופה" אשר תשמש לפתירת תופעת הקינאה הצולבת והייתרה תחולק לבעלים בהתאם לחלקיהם היחסיים בחבילת נכסים זו.

הסבר כיצד נוצרו תשלומי האיזון :

המערכת מחשבת מהו הערך שמגיע לכ"א מהבעלים על בסיס כלל הערכותיו לנכסים. לדוגמה , לבעלים 2 מגיע להערכתו 1,764 שהם 20% מהערכתו לכלל הנכסים( 8,820 ) כמוצג בטבלה. הואיל והוקצה לו נכס שלהערכתו 2,220 עליו לשלם תשלומי איזון של 456 (= 2,220-1764).

באופן דומה נערך החישוב לכל הבעלים.

3. קינאה צולבת ( Cross jealousy )

למושג קינאה קיימות הגדרות רבות . בעבודה זו אתייחס לאחת ההגדרות המתייחסות לעולם המקרקעין על בסיס חלוקת נכסים (הפרדת בעלות משותפת) בין קבוצת בעלים סגורה.

קנאה צולבת (cross-envy) היא מצב בחלוקת משאבים שבו אדם אחד מעדיף את החלק שניתן לאדם אחר, למרות שהקצאת החלקים בוצעה לפי העדפות סובייקטיביות של כל אחד. במובן זה, יש חציית העדפות – כלומר, אדם מעדיף את חלקו של מישהו אחר על פני שלו, גם אם ההקצאה נחשבת "צודקת" מבחינה פורמלית.

לפי הגדרות המודל בעבודה זו כל אחד מהבעלים , באופן דיסקרטי, מעביר למנהל החלוקה את רשימת ההעדפות שלו כמופיע בטבלה 1. בהליך ההקצאה לכל אחד מהבעלים מוקצית דירה על בסיס העדפותיו. אף לא אחד מהבעלים בקבוצה אינו יודע מהי טבלת העדפות של מי מיתר הבעלים. הוא יודע רק את העדפותיו בלבד. מה שכן יודעים הבעלים הוא  איזה נכס הוקצה לכ"א מיתר חברי הקבוצה.

בהתאם להעדפותיו שלו עצמו הוא מחשב את התמורה שניתנה לכל אחד מייתר חברי הקבוצה. היה ומי מיתר החברים קיבל ערך גבוה מהערך שהוא קיבל צצה ועולה הקינאה הצולבת.

בטבלה הבאה פרוט הקינאה הצולבת :

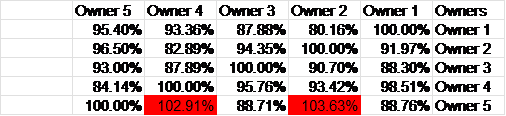
המשבצת שמול כל בעלים מייצגת באחוזים את מה שקיבל להערכתו ב-100%.המשבצות באדום מציגות את הקינאה של בעלים 2 ובעלים 4 בבעלים 5 אשר קיבל בהתאם להערכותיהם יותר מ-100% שהם קיבלו.

בערכי שווי תראה טבלה זו כך :

הסבר לטבלת הקנאה :

יש לחזור לטבלה בעמוד 6 לעיל.

לבעלים 2 הוקצה נכס שלפי הערכתו הוא 2,2,220 ותשלומי איזון לשלם 456 כך שהסכום נטו הוא 1,764 כרשום בטבלה בהצטלבות בעלים 2 ובעלים 2.

לעומת זאת בעלים 5 קיבל להערכתו נכס בשווי  2,030 ומשלם 202 תשלומי איזון כך שהסכום נטו לבעלים 5 הוא 1,828 .סכום זה , 1,828 שקיבל בעלים 5 להערכת בעלים 2  גבוה מהסכום שקיבל בעלים 2 לפי הערכתו , 1,764 . מכאן הקינאה הצולבת.

הסבר מפורט יותר כיצד נוצרת הקנאה הצולבת במודל:

הקנאה הצולבת (Cross-envy) נוצרת כאשר בעלים א' מעדיף את הנכס שהוקצה לבעלים ב , בהתבסס על הערכותיו הסובייקטיביות של בעלים א' עצמו.

שלבי היווצרות הקנאה הצולבת:

1. כל שותף מגיש את העדפותיו האישיות: הוא משנה את שומת השמאי כלפי מעלה לדירות שהוא רוצה, כלפי מטה לדירות שהוא סולד מהן, ומשאיר כפי שהיא לדירות שהוא אדיש לגביהן.
2. מתבצעת הקצאה שממקסמת את סך הערכים הסובייקטיביים: האלגוריתם ההונגרי בגרסת המקסימום משבץ כל שותף לנכס, כך שהערך הסובייקטיבי הכולל לכלל הבעלים הוא מקסימלי (יעילות פרטו).
3. נבדקת "שורת הקנאה":
   כל שותף יודע איזה נכס קיבל כל אחד מהאחרים, וגם את תשלומי האיזון שלהם. הוא מחשב את שווי הדירה נטו  שקיבל האחר ומחשב לפי הערכתו האישית (ולא של אותו אחר) את השווי שהאחר קיבל  כולל תשלומי איזון.
4. דוגמה מהמאמר:
   • בעלים 2 קיבל שווי נטו של 1,764 (דירה שקיבל לפי ערכתו: 2,220 פחות 456 איזון).
   • בעלים 5, לפי הערכת בעלים 2, קיבל את הדירה ששוויה לפי הערכתו  2,030 פחות 202 = 1,828.
   • מאחר ו־1,828 גבוה מ-  1,764  בעלים 2 "מקנא" בבעלים 5.
5. המערכת מזהה את הקנאה באופן אוטומטי ומפעילה את מנגנון התיקון מתוך "הקופה".

בשלב זה המערכת תשתמש בכסף "שבקופה " 566 אלפי ₪ לסילוק הקינאה.

לסילוק הקינאה ביצעה המערכת במקרה זה שלשה סבבים עד לסילוק הקנאה לחלוטין וחלוקת יתרת הסכום הנותר בין הבעלים. בכל בסבב נבדק מחדש האם נפתרה הקינאה הקודמת והאם נוצרה קינאה חדשה. חלוקת התמורה בקופה תקטין את תשלומי האיזון למי שחייב בתשלומי איזון ותגדיל את הסכום למי שמגיעים תשלומי איזון.

לאחר מכן לא תשרור יותר קינאה וכל אחד מהבעלים יקבל יותר ממה שחשב שמגיע לו לפי הערכותיו.

להלן טבלת ההקצאות הסופית :

כתוצאה מהתהליך כל אחד מהבעלים קיבל באחוזים יותר ממה שמגיע לו בין 4.68% לבעלים 5 ועד 8.48% לבעלים 2.

טבלת הקינאה הצולבת תראה כך לאחר ביטולה :

בירוק רשום הערך שכ"א מהבעלים קיבל לפי הערכותיו. לדוגמא, בעלים 1 קיבל להערכותיו הסובייקטיביות 1,768 אלפי ₪. חוץ מבעלים 4 שקיבל להערותיו סכום דומה אף לא אחד מיתר הבעלים קיבל יותר ממנו.

החלוקה המוצעת במאמר זה היא חלוקה יציבה ולאיש אין יתרון כלכלי להתחלף עם מי מיתר הבעלים.

4. לכאורה בשלב זה אמור הייתי לסכם המאמר אולם מצאתי כמה נושאים שעליהם יש להרחיב הכתיבה :

הנושא הראשון הוא מצב שלעיתים רחוקות ונדירות עלול להיווצר בו קופת "פרדוקס הערך" לא תספיק כדי לחסל את כל הקנאה הצולבת.

במקרה זה המערכת בנויה כך שהיא תיצור מצב של "כמעט חלוקה ללא קינאה" (ε-envy-free allocation או almost envy-free allocation). הצדדים יכולים לבחור אחוז מינימלי של קינאה מותרת (%ε ) ואז להריץ מחדש את האלגוריתם. במקרה זה המערכת תסמן את הקינאה באדום חלש להדגיש כי היא קיימת אולם היא מינימלית.

הנושא השני הוא ההנחה בדבר יחס הבעלים לנושא הסיכון. הנחת העבודה הבסיסית בשיטת חלוקה זו היא כל הבעלים אדישים לסיכון או שונאי סיכון. אדם האדיש לסיכון יהיה אדיש אם יקבל את מלוא הערך דרך נכס או באמצעות נכס בשווי נמוך יותר והייתרה במזומן כל עוד השווי הכולל זהה. שהרי מדובר בחלוקת נכסים מוחשיים.

אדיש לסיכון (risk neutral) הוא אדם שמעריך תרחישים רק לפי תוחלת הערך שלהם, בלי להתחשב ברמת הסיכון או אי הוודאות.

שונא סיכון (risk averse) הוא אדם או שחקן כלכלי שמעדיף תוצאה ודאית על פני תוצאה לא ודאית גם אם תוחלת הרווח של האפשרות הלא ודאית גבוהה יותר.

הנושא השלישי ואולי המעניין ביותר, מה היה מצב הקינאה אילו הקצאת הנכסים הייתה בדרך של הגרלה. שהרי אחת המטרות של מאמר זה להציג את שיטת ההגרלה הנהוגה כיום במשק ישראלי באור השלילי ביחס לקנאה והקיפוח הסובייקטיבי  שבו היא פועלת.

לצורך ההדגמה נשתמש במערכת בהתאם להעדפות האישיות של הבעלים כמוצג לעיל. סדר בחירת הנכס לכל אחד מהבעלים יעשה בדרך של הגרלה. הבעלים שיצא ראשון בהגרלה ,השני אחריו. הבעלים האחרון, החמישי בדוגמה שבמאמר, יקבל את הנכס שלא נבחר.

סדר ההגרלה שעלה בגורל בעלים מספר 1 יהיה הראשון לבחור, בעלים מספר 2 השני ובחור וכך הלאה.

בטבלה הבאה בחירת הבעלים 1 עד 4.

ההנחה בבחירת כ"א מהבעלים היא זו המקיימת את התנאי כי  ההפרש בין הערכתו האישית ביחס להערכת השמאי תהיה מקסימלית. בבחירה זו תשלומי האיזון שלו יהיו לפי השומה באופן  שהרווח העודף  שלו יהיה מירבי..

לדוגמה : לפי הערת השמאי מגיע לכ"א מהבעלים 1,723 אלפי ₪. בעלים 1 בחר בנכס 2 שבו הרווח לפי העדפותיו הוא 150 שלפי ₪. תשלומי האיזון שבעלים 1 צריך לשלם הם 77 אלפי ₪ (1,800-1,723 = 77 ).הרווח הרעיוני שלו הוא לכן 150-77 = 73 אלפי ₪)

בעלים 5 (קיבל את הנכס שנשאר) בפועל  קיבל נכס ועוד תשלומי איזון בסך 1,723 אלפי ₪ לעומת הסכום לפי הערכותיו שאמור היה לקבל 1,828 אלפי ₪. ההפסד הרעיוני של בעלים 5 הוא לכן 1,828-1723=105 אלפי ₪.

זהו שנאמר ראשון זוכה אחרון בוכה.

הנושא הרביעי הוא הצעת שיטה למניעת ניצול לרעה של המערכת ע"י ניפוח או ספקולציות בערכים הסובייקטיביים:

השיטה קובעת כי סה"כ שווי הנכסים לפי הערכת השמאי תשמש תנאי מוחלט לסה"כ  השווי הסובייקטיבי של כל אחד מהבעלים. כ"א מהבעלים יוכל לסדר את הערכותיו הסובייקטיביות בתנאי שסכומן יהיה זהה לזו של השמאי.

הנושא החמישי הוא הסבר על תחילת תורת חלוקת העוגה ( בת כ-70 שנה בלבד) וארבעה מאמרים רלוונטיים לעבודה זו.

אבי תורת חלוקת העוגה נחשב המתמטיקאי הוגו שטיינהאוס Hugo ) Steinhaus)    יהודי פולני, שפעל בשנות ה־40 של המאה ה־20. יום אחד, לפי המסופר, שמע שיחה ברחוב בין שני אנשים שהתלבטו כיצד לחלק עוגה בצורה הוגנת, וזה עורר בו עניין מתמטי. הוא העלה את הרעיון של חלוקה שתהיה "הוגנת" (fair) – כלומר, שכל צד יקבל לפחות את מה שלדעתו שווה מחצית מהשלם".

רעיון זה הוליד תחום שלם במתמטיקה, כלכלה ותורת המשחקים שעוסק רק בחלוקת משאבים ממשיים: קרקעות, ירושות, זמן, כספים ועוד. בהמשך הצטרפו חוקרים רבים והתחום התרחב לתוך מחשוב, אתיקה, מדיניות ציבורית

שטיינהאוס שיתף את חבריו המתמטיקאים, ביניהם סטניסלב אולם וסטפן באנך ויחד הם פיתחו שיטות לחלוקה הוגנת, בראשן שיטת "אחד חותך – השני בוחר" (Cut and Choose) שמבטיחה שלפחות צד אחד לא יקנא בשני.

(למעשה התיעוד הכתוב הראשון לשימוש בשיטה זו היה אברהם אבי האומה מול רועי לוט כפי שנאמר " "הֲלוֹא כָל הָאָרֶץ לְפָנֶיךָ הִפָּרֶד נָא מֵעָלָי: אִם  הַשְּׂמֹאל וְאֵימִנָה, וְאִם הַיָּמִין וְאַשְׂמְאִילָה" בראשית י"ג, ט')

.

להלן תקציר ארבעה מאמרים קרובים לשיטה המוצעת במאמר זה :

Aronson, J., Ben-Akiva, M., & Lerman, S. (1985). "Fair Assignment Algorithms."

מאמר זה מציע אלגוריתמים לחלוקה הוגנת של משימות או משאבים כאשר קיימות העדפות שונות בין שחקנים. אחת מהשיטות המוצעות מבוססת על התאמה בין שחקנים לבין פריטים באופן שמביא למקסימום שביעות הרצון המשותפת – מטרה שדומה מאוד למה שמושג דרך האלגוריתם ההונגרי בגרסתו הממקסמת.

Budish, E. (2011). “The Combinatorial Assignment Problem: Approximate Competitive Equilibrium from Equal Incomes.”

פרסום: Journal of Political Economy, Vol. 119, No. 6

במאמר זה, E. Budish מתמודד עם בעיית חלוקה של טובין בלתי ניתנים לחלוקה (indivisible goods)  בקרב שחקנים עם העדפות שונות. הוא מציע מודל שנקרא:

A-CEEI = Approximate Competitive Equilibrium from Equal Incomes

• כל שחקן מקבל "הכנסה" זהה ויכול להשתמש בה כדי "לקנות" צרורות של טובין על פי העדפותיו.
• המחירים מותאמים כך שיתקרבו למצב של שיווי משקל תחרותי, אבל בשל אי האפשרות לפצל טובין – מדובר רק בשיווי משקל בקירוב.

Brams, S. J., & Taylor, A. D. (1996). Fair Division: From Cake-Cutting to Dispute Resolution

ספר זה נחשב אב-טיפוס של תורת חלוקה הוגנת (Fair Division). הוא עוסק בדרכים מתמטיות ופרוצדורליות לחלק משאבים בין שחקנים כך שאף אחד מהם לא יקנא באחר – כלומר, שכל אחד יעדיף את חלקו על פני חלקו של אחר.

המחברים מציגים מגוון שיטות, כולל:

1. חלוקת עוגה קלאסית – במובן המתמטי, שם נדרש לחתוך משאב רציף בין כמה שחקנים.
2. שיטת Adjusted Winner – עבור שני שחקנים, המובילה לפתרון יחיד שהוא גם יעיל, הוגן ונטול קנאה.
3. אלגוריתמים פרקטיים – לחלוקה גם של משאבים בדידים, כגון ירושות, אדמות או נכסים.

סיכום :

המודל שלפנינו מתמודד עם אחת הבעיות הקשות והמוכרות בתחום חלוקת רכוש – חלוקה הוגנת של נכסים מוחשיים בלתי ניתנים לחלוקה פיזית או משפטית, תוך מניעת קינאה ותחושת קיפוח בקרב הבעלים. המודל שהוצג, המבוסס על מקסום הערכות סובייקטיביות ובחינה מחזורית של קינאה צולבת, הוכיח את עצמו ככלי מתמטי ואנושי גם יחד. הוא מניח תשתית חלוקתית שהיא בעת ובעונה אחת הוגנת, יציבה, נטולת קינאה, ויעילה פרטו.

ייחודיותו של המודל אינה רק בפתרון האלגוריתמי אלא ביכולתו להביא לתחושת שביעות רצון קולקטיבית, גם כאשר מדובר בנכסים מורכבים רגשית וכלכלית כמו דירות. השימוש ב"פרדוקס הערך" כמשאב לפתרון קונפליקטים מציע גישה מקורית: דווקא מהמגוון והפערים נוצרת יתרת ערך – ונעשה בה שימוש לריפוי השברים.

ראינו גם שהשיטה מתמודדת היטב עם מצבים מורכבים, אי  שוויון במספר הנכסים והבעלים ואחוזי בעלות שונים, אפשרות ליתרת קנאה מזערית, ואף תמריצים פסיכולוגיים למניעת מניפולציה, תוך שמירה על מנגנון בקרה פנימי.

כמענה לשיטת ההגרלה הנהוגה כיום, מציע המודל פתרון מדויק ואלגנטי שמעדיף שיקול דעת על פני מקריות, צדק כלכלי על פני מזל עיוור, והוגנות ניתנת להוכחה מתמטית על פני תחושת "גורל".

בסופו של דבר, המודל המוצג כאן אינו רק כלי טכני – הוא הצעה לדרך חדשה להבנה מהי הוגנות בחלוקה, כיצד ניתן לכמת אותה, ולבסוף – כיצד ניתן להשיגה.

לא אוכל לסיים ללא הכרת תודה לחברי המתכנת בחסד חיים קושיצקי שהאזין ופתר ובתכנה את כל הבעיות שעלו במעלה ההר עד להשלמת תכניה ייעודית שיודעת לפתור ההקצאה ופתרון הקינאה הצולבת לכל מספר בעלים או נכסים ולאחוזי בעלות שונים.